Today I’m going to talk about parallel parking. We’ve all had to do it at some point (at least, those who drive) and certainly we’ve all noticed how much of a pain it is to get into a small space. Well, as it happens, if your car has length 
So what does this rely upon? Well, we’re going to have to talk about Lie Groups to do this. A Lie Group is a group that is also a manifold, and such that the multiplication and inversion maps are smooth. Lie groups turn out to be incredibly nice geometric objects, as well as a nice group. However, the particularly nice properties of Lie groups aren’t the big feature here.
The important feature here is that if you take the tangent space to the origin of the Lie group’s manifold, you get a natural Lie algebra under commutator of vector fields. It turns out that for “nice” Lie groups, there is a very precise correspondence between the Lie algebra and the Lie group. What this means is that we can take problems about a Lie group and solve them in the Lie algebra. We then get back to the group through the exponential map, 
Now let’s look at the parallel parking problem, and add more background merely as needed. We first need to translate the car into mathematics. We do this by first assuming that the car is of unit length (for simplicity) and taking 
This makes the configuration space of the car into 
Now, there are some important vector fields on this manifold (which is also a Lie group, and so we can just work with the vector fields and use the Lie algebra to park). The first one is called Steer, and all it does is change the direction of the front wheels infinitesimally. It can be expressed as 
So this turns out to be a nasty computation which can be done with the aid of a diagram, a name for the infinitesimal distance, and a LOT of care, but the up side is that Drive
![.[\mathrm{Steer},\mathrm{Drive}]=-\sin(\phi+\theta)\frac{\partial}{\partial x}+\cos(\phi+\theta)\frac{\partial}{\partial y}+\cos\theta \frac{\partial}{\partial \phi}](https://s0.wp.com/latex.php?latex=.%5B%5Cmathrm%7BSteer%7D%2C%5Cmathrm%7BDrive%7D%5D%3D-%5Csin%28%5Cphi%2B%5Ctheta%29%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+x%7D%2B%5Ccos%28%5Cphi%2B%5Ctheta%29%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+y%7D%2B%5Ccos%5Ctheta+%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+%5Cphi%7D&bg=ffffff&fg=333333&s=0&c=20201002)
So what we really want to do when we parallel park is to slide sideways. This vector field is given by 
Now that we’ve shown that you CAN parallel park, I don’t recommend trying to follow this procedure in a tight space, simply because parking in tight spaces is tough, and best avoided. I’ll just continue using public transportation, myself…
Charles Siegel
Jim Stankewicz
Matt DeLand
Rigorous Trivialities 
Great post ! helps me understand the commutator so much better. And now when I’m sitting in a car with someone who’s struggling, I can helpfully suggest computing a commutator on the Lie algebra ;)
Pingback: Ars Mathematica » Blog Archive » Parallel Parking at Rigorous Trivialities
Alternate headline:
Commutators for Commutors!
I can’t say I understand the math, but you state: “… and \theta to be the angle between the front axle and the line AB, counterclockwise.” However, as I understand it, the front axle of a car is always perpendicular to AB, steering is done by shifting the wheels in-place. This differs from how I understand your design in that if the wheels were rotated 90 deg (which they can’t), they would lie along the same track, whereas on your car it seems they would lie on two parallel tracks separated by the front axle.
Maybe this makes no difference to the math, but I just thought I’d point it out.
I am treating the car like it is turned by moving the front axle rather than just turning the wheels, and that if
degrees, the axle is perpendicular to the body, so to get the intuitive coordinates requires a translation along the torus, and so the equation 
would be after translating the coordinates to make the perpendicular into 0. However, as we only looked at infinitesimal motions, none of these affect the proof, and so I omitted discussing them for simplicity. Perhaps it would have been better had I drawn a picture and put it into the post, but it didn’t occur to me at the time.
Well Charles, you’ve scooped me! I’ve had a parallel parking / contact geometry post in the works for a bit, but I’m not totally happy with it yet. Maybe it is in the air right now & we can get an interblog geometric PDE party going on…
(nice post, by the way!)
Pingback: Parallel Parking and the Geometry of Differential Equations « The Everything Seminar
There’s a version of this in Burke’s Applied Differential Geometry, right?
But still: great post.
That looks similar, I’d need to spend some time to see if it’s quite the same thing. I haven’t studied holonomy yet. The version I have seen before is in Rossman’s “Introduction to Lie Groups” and though I haven’t looked at it in awhile, I think that the post is mostly rephrasing and expositing the example from this book.
The logical next question is: how many times do you have to go through this “wriggle, drive, reverse wriggle, reverse drive” sequence in order to park in a given spot? I think it’s proportional to 1/ε2 — if the slack in the parking space is half the size it should take four times as many maneuvers to park. (Basically, the circular arcs that the curve traverses can be approximated by parabolas.) But I haven’t worked out the details.
That is the right order of magnitude since you need up move “up the contact field” and the amount which you move up is proportional to the area bounded by the curve which describes your motion in (x,y,p)-space, projected into the (x,p)-plane. This is essentially due to the fact that the derivative of the contact form
is the area form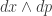 
on the position/momentum plane.
Also: is there any other field where the clauses pile up qui
(comment died)
…where the clauses pile up quite so precariously? Sometimes I feel like I’m almost hitting stack overflow when trying to make a precise statement…
In the early 90’s I came across the Nelson book example and thought it would be a great example for a mathematical physics class I was teaching at Swarthmore College. However, I got stuck in trying to prove that the commutators of Steer, Drive, Wriggle and Slide were closed.
I just spent a few minutes trying to find out where my difficulty was and it relates to the commutator of Drive and Slide. I cannot get it to be a linear combination (with constant coefficients) of the four operators above.
Did I make a calculation mistake? Am I incorrect in believing that a Lie algebra requires the commutators to be closed? This has stuck in the back of my head for years so a clarification would be most welcome.
I think I might have a typo, and it’s going to be one that’s a pain to hunt down…Drive and Slide are supposed to commute, but when I check the commutator I got something that’s nonzero. However, the point remains that this general idea works, even if I have made a mistake somewhere in the specifics…I’ll edit (and mark the post as edited) if I can find time and track down the mistake and put all the details right again.
What kind of mathematical argument is to say “the point remains” in spite of the fact that you cannot get Drive and Slide to cancel out? Why should the idea work out? Because you say so? because Nelson says so? because Rossman says so?
I did not present the idea in my lectures precisely because I could not confirm that the commutators formed a Lie group. Appeals to it “should work out” without being able to do so are not going to help us clarify the issues involved.
You could at least acknowledge that there is indeed something wrong and clarify that indeed, a Lie algebra requires that all commutators be linear combinations of the members in the algebra so this merits more investigation. What if none of us made a typo and this particular implementatio of the idea has been wrong all these years? Let’s try to figure out where the problem is instead of throwing in the towel.
It was borne out of confidence that I’d be able to fix the problem without too much effort. And now that I’ve spent most of the evening working on it instead of on my homework (bad me!) I’ve not come up with a real solution. For any GIVEN
, I can do it, using 
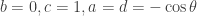, where these are the coefficients with respect to Steer, Drive, Wriggle, Slide as an ordered basis, even though I was certain that the commutator should vanish, which it only will when 
. I’m out of ideas, because I couldn’t find an error in the derivations of what the vector fields should be, and working all the linear algebra forced nonconstant coefficients upon me. Anyone else got something, or shall this go into my list of spectacular public mistakes, along with an attempt to prove uniformization via Ricci flow (following Hamilton) in a seminar?
Also, my vector fields agree with Nelson’s and Rossman’s, so that means that we’re all making the same mistake somewhere, because both seemed confident that Drive and Slide commute.
I’m not so sure that Drive and Slide should commute. As you observe, they will commute in special cases. For example, if there is no steering (the wheels are pointing straight). But if there is steering I can sort of see that the commutator would lead to the car being displaced backward which is what I get when I calculate the commutator.
So I come back to my original questions. Is it the case that a Lie algebra requires that all commutators be constant coefficient linear combination of group members? If that is the case maybe the problem is that we have not identified all the group members.
Ahh! Now I know what I was thinking! Though yes, the lie algebra has to be able to express things in terms of constant real coefficients, we don’t need to know all of the elements. Nelson and Rossman claim that it’s a four dimensional Lie algebra, and that is their mistake, it’s larger. However, the real point was that Slide can be written in terms of commutators of Steer and Drive, so that it lies in the Lie algebra, rather than that Drive, Steer, Wriggle and Slide span it. You don’t need to be able to perform every conceivable action in your car, you just need to know that you can (somehow) translate sideways. Joe and I were talking about it late last night and we figured out that that was my original intention with the comment.
I’m pretty sure Drive and Slide should not commute in general. To see this, imagine that your steering wheel is turned to some nonzero angle theta. If you begin driving, you’ll follow some circular arc centered at some point. Say you drive for some finite time,
, and then slide. Now reverse drive will follow the same circular arc (in the opposite direction) but translated over so it’s centered at a new point. Finally, after reverse driving, you reverse slide. If Drive and Slide commuted, you would always end up where you started, but in general this doesn’t happen: You did a reverse drive along a circular arc between your slide and reverse slide. This changed the orientation of your car, and so your slide and reverse slide were not in opposite directions. What we get instead is that the result should be some translation of the car in the xy-plane, so we expect that in general: [Drive, Slide] = 
, which is what we get by computing.
As for the other issue, it is true that Drive and Steer generate a Lie algebra. The fact that some commutators are not constant coefficient linear combinations of Drive, Steer, Wriggle, and Slide only implies that this Lie algebra is not 4-dimensional–We have not found a complete set of generators. One may raise the argument that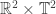
is a four-dimensional Lie group and so should have a four-dimensional Lie algebra. However, our vector fields are not in the Lie algebra of 
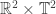; this Lie algebra is abelian and we have a lot of non-vanishing commutators. What I think is happening is this: There is some Lie Group 
that represents everything you can do with a car by driving and steering. We don’t know what dimension 
is, but we do know that it acts on the states of your car 
. What our formulas for Drive, Steer, etc. give is a realization of the Lie algebra 
as the infinitesimal action of 
on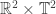 
. It is possible that Drive and Steer only generate a subalgebra of 
, but that is ok. All we really wanted to know is that Slide is in this subalgebra, as Charlie has shown. We aren’t really interested in the rest of the algebra or its dimension.
There is one caveat, though. We have only talked about the Lie algebra, assuming it corresponds to some Lie group. The existence of this group does not follow immediately if the Lie algebra is infinite-dimensional. As a student of physics, I tend to believe that there is a corresponding Lie group in this case. Anything I can do with my car by driving and steering I can undo by driving and steering. Still, it would be nice to know what the dimension of the Lie algebra is, so we can rigorously put the subject to rest.
Thank you, jwwalsh, for your post. It clarifies the issues involved tremendously. I’ve been waiting 15 years for it.
I get exactly the same outcome as jwwash: you get a Lie algebra of countably infinite dimension: you can keep getting arbitrary high powers of $\cos\theta$, $\sin\theta$ times forward slide and side slide. So I agree with you: we cannot find the Lie group that acts on the car configuration space by the methods of Nelson and Burke. Rossmann makes a direct copy BTW. Anyhow, you can solve the problem by leaving the steering angle out of the configuration space and instead saying that a general transformation available to the driver is of the form $\exp(s(D + \kappa\,R))$, where $D$ drives the car forwards, $R$ rotates it about the midpoint of its hinder axle and now you say that $\kappa$, the curvature of the car’s path is now a “control force”, a parameter that parameterises the family of basic transformations. So our configuration space is now $\mathbb{R}^2\times\mathbb{T}^1$ comprising the car’s $x,\,y$ position and its heading $\phi$. You can clearly get from $x,y,\phi$ to any point in Nelson’s / Burke’s configuration space $\mathbb{R}^2\times\mathbb{T}^2$ by imparting a drive angle. It is then a fairly simple matter to prove that the smallest Lie group containing the basic transformations of the form $\exp(s(D + \kappa\,R))$ is indeed $\mathbb{E}(2)$, the Euclidean group of all orientation preserving isometries of the plane: rotations and translations. See my calculations at http://www.wetsavannaanimals.net/wordpress/lie-theoretical-systems-theory
My calculation for the commutator [Drive,Slide] is equal to $-\sin\theta\left(\cos\phi \frac{\partial}{\partial x} + \sin\phi\frac{\partial}{\partial y}\right)$. This looks to me like a back sliding (the negative sign) operator that preserves the steering angle $\theta$. So shouldn’t we talk about SideSlide and FrontSlide, instead of just Slide?
Also, couldn’t the same operation be performed by -Steer, Reverse, +Steer?
On a more theoretical note, how does one usually prove that a Lie algebra is closed? By brute force calculation?
Pingback: Carnival of Math #18 « JD2718
In environments where contact between bumpers is not a problem, we have positive examples with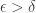
where delta can be quite small. If we waive the “no exchange of paint” requirement, delta approaches 0. I’ve personally left three fingers behind, and contact in front (that would be about 2-3″).
Arbitrarily small movements are not possible, but rolling the enclosing cars makes up for it..
This interesting post is not quite correct. “Slide” is made up of 8 operations,
Steer, Drive, Reverse Steer, Drive,
Steer, Backup, Reverse Steer, Backup
This actually works, see William Burke’s excellent text, referenced in a comment above.
I took Bill Burke’s differential geometry class at UC Santa Cruz, lo these many years ago.
Pingback: Chapter 13: Lie Theoretical Systems Theory | Wet Savanna Animals
Pingback: Parallel Parking a Car | Wet Savanna Animals
Very old but interesting post :) Although I think some theoretical mistakes in the post.
Reblogged this on phylyd.
Re-read this post after @seanmcarroll blogged about Drive and Steer giving you Slide. My cursory reading of William Burke’s book, claimed by a reply above to correctly solve the problem, reveals that it merely asserts the same things as Nelson’s book and incorrectly states that the Lie algebra, as defined, is 4-dimensional.