Locally Free Sheaves and Vector Bundles

Last time, we talked about sheaves of modules, and focused on the correspondence between sheaves of ideals and subvarieties. We were talking about the internal geometry of the variety. Today, we’ll talk a bit about more external geometry. Specifically, we’ll talk about how sheaves give us new varieties $E$ with maps to $X$ whose fibers are all vector spaces. In fact, they’ll look locally like open sets of $X$ times a vector space. Such objects are called vector bundles, and are rather closely tied to the theory of sheaves of modules on $X$ .

We call a sheaf of modules $\mathscr{F}$ free if it is isomorphic to a direct sum of copies of $\mathscr{O}_X$ . We call the number of copies of $\mathscr{O}_X$ the rank of the free sheaf. Now, we will call a sheaf locally free if there exists a cover of $X$ by open sets (we don’t require them to be affine) such that $\mathscr{F}|_U$ is a free $\mathscr{O}_X|_U$ -module. Note that a locally free module is automatically quasi-coherent, and is coherent if it has finite rank. If $X$ is connected, then the rank is the same everywhere.

A quick algebraic comment is in order: the coherent sheaf associated to a finitely generated module $M$ is locally free if and only if it is a projective module, that is, there exists $N$ such that $M\oplus N$ is free. Though beware, if we were working with schemes instead of varieties, we need to be more careful about this. But we’re focusing on varieties right now, so everything’s ok.

Now let’s look at things from the other direction. As mentioned earlier, if $X$ is a variety, a vector bundle over $X$ is a variety $E$ with a map $\pi:E\to X$ such that the following conditions hold:

For each $p\in X$ , we have $\pi^{-1}(p)$ is isomorphic to $\mathbb{A}^n$ for some $n$
There exists a cover $U_i$ of $X$ such that $\pi^{-1}(U_i)$ is isomorphic to $U_i\times \mathbb{A}^n$ .

We note quickly that if $X$ is connected, then we can use the same $n$ at each point, and say that the vector bundle has rank $n$ .

So now lets do some examples of each. For any variety $X$ , there is a vector bundle $E=X\times \mathbb{A}^n$ for each positive $n$ . This is called the trivial vector bundle. Other vector bundles are easiest to describe by using locally free sheaves, once we’ve described the correspondence. But first, some examples of locally free sheaves. Fix an integer $d$ . Then we define the locally free sheaf of rank one on $\mathbb{P}^n$ called $\mathscr{O}_{\mathbb{P}^n}(d)$ to be the one taking each open set $U$ to the set of ratios of homogeneous functions $f/g$ such that $g$ is nonzero on $U$ and $\deg f-\deg g=d$ . This is locally free, because if we restrict to a standard copy of affine space, we are then looking at $U\subset \mathbb{A}^n$ is assigned $f/g$ rational functions defined everywhere on $U$ , that is, we get precisely $\mathscr{O}_{\mathbb{P}^n}|_{\mathbb{A}^n}$ .

So on to the correspondence. If we take $E\to X$ a vector bundle, there is a relatively simple way to construct a sheaf. Assign to $U$ the collection of morphisms $s:U\to E$ such that $\pi\circ s$ is the identity on $U$ . This sheaf will be locally trivial, and the open sets we use can be the ones for which $\pi^{-1}(U_i)\cong U_i\times\mathbb{A}^n$ . This is because on these sets, we’re looking at functions $U_i\to U_i\times\mathbb{A}^n$ which compose with the projection to give the identity. This is the same as looking at morphisms $U_i\to \mathbb{A}^n=\mathbb{A}^1\times\ldots\times\mathbb{A}^1$ , which is just a list of $n$ regular functions on $U_i$ . So a vector bundle defines a locally free sheaf.

So now we start with a locally free sheaf $\mathscr{F}$ of rank $n$ . Pick an open cover of $X$ such that $\mathscr{F}|_{U_i}$ is free for each $U_i$ in it. We can choose the open cover to be finite, because varieties are quasi-compact. So now we take the disjoint union of $U_i\times\mathbb{A}^n$ for all $i$ . So now we have one isomorphism $\mathscr{F}|_{U_i}\to \mathscr{O}_{U_i}^n$ and another $\mathscr{F}|_{U_j}\to \mathscr{O}_{U_j}^n$ . Restricting each of these to $U_{ij}=U_i\cap U_j$ (we will use this convention from here on out) we get two different isomorphisms $\mathscr{F}|_{U_{ij}}\to \mathscr{O}_{U_{ij}}^n$ , and we will denote them by $g_i,g_j$ . We then get $g_{ij}=g_j g_i^{-1}$ , an automorphism of $\mathscr{F}|_{U_{ij}}$ . Now, by the isomorphism with $\mathscr{O}_{U_{ij}}^n$ , we can identify this with an $n\times n$ matrix of regular functions on $U_{ij}$ .

So now we glue. We take $U_i\times\mathbb{A}^n$ and $U_j\times\mathbb{A}^n$ and identify them along $U_{ij}$ by the map which takes $(x,v)\in U_{ij}\times\mathbb{A}^n$ to $(x,g_{ij}(v))$ . So now we perform this for all $i,j$ , and call this object $E$ , and it comes with a map $E\to X$ by forgetting the vector coordinate on any point. So the fibers are now copies of $\mathbb{A}^n$ and by construction, around each point there’s a neighborhood on which the space is $U\times\mathbb{A}^n$ . So all we need to do in order to check that this is a vector bundle is to check that it is a variety. It certainly has an open cover by affine varieties, again by construction, and in fact this cover is finite. The rest follows from the fact that $g_{ij}\circ g_{jk}\circ g_{ki}$ is the identity map. So we’ve now established a correspondence between locally free sheaves and vector bundles.

Next time, we’ll further investigate a special class of these, the line bundles. That is, vector bundles of rank one. The associated locally free sheaves are called invertible sheaves, because we’re going to make a group out of them, which means that each will have an inverse.

About Charles Siegel

Charles Siegel is currently a postdoc at Kavli IPMU in Japan. He works on the geometry of the moduli space of curves.

View all posts by Charles Siegel →

9 Responses to Locally Free Sheaves and Vector Bundles

John Armstrong says:

April 11, 2008 at 2:51 pm

You’ve shown two constructions, but in what sense is it a correspondence? If you mean it’s an equivalence — that the two constructions invert each other (up to isomorphism) — then you need to show that. If you mean it’s an adjunction you need to show that too.
Charles says:

April 11, 2008 at 3:07 pm

It is a correspondence up to isomorphism, yeah. A fairly quick way to see it is that you can take a locally free sheaf and then construct a vector bundle out of it, but then the sheaf of local sections over each trivializing set are determined, and they agree on overlaps. A standard exercise is that given an open cover and sheaves on each element which agree on overlaps, there is a unique sheaf which restricts to them. For the other direction, use the trivializing open cover for the sheaf of sections, and it glues together using the transition maps for the vector bundle.

It does require a bit of checking, but it’s not too difficult to do it.
Pingback: Serre Duality « Rigorous Trivialities
Bob says:

January 24, 2009 at 11:00 am

In the penultimate paragraph, what do you mean by g_ij(v)? g_ij both an automorphism of the sections of F on the intersection of Ui and Uj and correspondingly an nxn-matrix of regular function on the intersection. how does this act on v– a point in A^n to give another point in A^n?

Thanks for these blogs. I’ve struggled to find an explicit comparison of sheaves and bundles like this.
- Alex says:
  
  October 10, 2009 at 9:11 am
  
  Have look at Hartshorne p.128 ex. 5.18.
Charles Siegel says:

January 24, 2009 at 6:36 pm

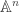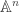It acts as the $n\times n$ matrix, think of $\mathbb{A}^n$ as vectors. So it will, for instance, identify the origins of both copies of $\mathbb{A}^n$ .
Stefano says:

April 12, 2009 at 3:25 am

In property (2) of a vector bundle, wouldn’t you need that the isomorphism commutes with the projection?
Pingback: K-Theory Seminar in Basel « ⍵-Category Tea
Pingback: More on Sheaves | Theories and Theorems

Comments are closed.

S	M	T	W	T	F	S
« Mar				May »
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30

	Francisco Palmios on Gradings of Rings and Mod…
	Anonymous on The Veronese Embedding
	Varieties and Scheme… on Schemes
	Varieties and Scheme… on Abstract Varieties
	Rena on Sheaves