Kontsevich’s Formula

Posted on December 23, 2008 by Charles Siegel

This is my last post of 2008, so happy holidays to everyone!. This one shouldn’t take too long, it’s just applying the lessons of the last few posts to compute some numbers. We start by talking like physicists. We’ll write \Phi(y)=\Phi_{c}(y)+\Phi_q(y), the classical and quantum parts. The classical part has the \beta=0 terms. We don’t really care about them. The quantum part only actually appears in its third derivatives, and so we can modify things by quadratic terms.

This modification lets us replace the quantum part of \Phi by \Gamma(y)=\sum_{n_{p+1}+\ldots+n_m\geq 0} \sum_{\beta\neq 0} N(n_{p+1},\ldots,n_m;\beta)\prod_{i=1}^p e^{\left(\int_\beta T_i\right)y_i}\prod_{i=p+1}^m \frac{y_i^{n_i}}{n_i!}.

Taking the i,j,kth third partial gives \Phi_{ijk}, so we can use the somewhat nicer form \Gamma in our calculations.

Now, the example! Look at \mathbb{P}^2. Then A^*\mathbb{P}^2 has a basis T_0=1, T_1=\ell and T_2=pt. Then we have g=\left(\begin{array}{ccc}0&0&1\\ 0&1&0\\1&0&0\end{array}\right).

This tells us that T_i*T_j=\Gamma_{ij0}T_2+\Gamma_{ij1}T_1+\Gamma_{ij2}T_0. As T_0 is the identity element of the quantum cohomology ring (call it H_Q^*(X)), the product is determined by the following:

\begin{array}{rcl}T_1*T_1&=&T_2+\Gamma_{111}T_1+\Gamma_{112}T_0\\T_1*T_2&=&\Gamma_{121}T_1+\Gamma_{122}T_0\\T_2*T_2&=&\Gamma_{221}T_1+\Gamma_{222}T_0\end{array}

This tells us that (T_1*T_1)*T_2=(\Gamma_{221}T_1+\Gamma_{222}T_0)+\Gamma_{111}(\Gamma_{121}T_1+\Gamma_{122}T_0)+\Gamma_{112}T_2, and also T_1*(T_1*T_2)=\Gamma_{121}(T_2+\Gamma_{111}T_1+\Gamma_{112}T_0)+\Gamma_{112}T_1.

Now, associativity says that these are equal, so, in particular, the coefficients of T_0 are equal. So we get the equation \Gamma_{222}=\Gamma_{112}^2+\Gamma_{111}\Gamma_{122}.

Now, recalling our notation frombefore, we set \beta=d\ell, and N_d=N(n,d), because these are zero unless n=3d-1. Why is this? Because N(n,d) is the number of degree d curves passing through n points in the plane. Now, teh dimension of the space of degree d plane curves with \delta nodes is \binom{d+2}{2}-\delta-1, and the number of nodes required to make a degree d curve rational is \binom{d-1}{2}. Computing this, we get 3d-1.

So we’ve set N_d=N(3d-1,d), and these are all the potentially nonzero Gromov-Witten invariants that we can talk about (the positive genus case is harder, and my understanding is that it does require stacks).

Anyway, this discussion lets us write \Gamma(y)=\sum_{d\geq 1} N_d e^{dy_1}\frac{y_2^{3d-1}}{(3d-1)!}. So now we must compute the third derivatives of this, at least the ones appearing in the formula above. We get

\begin{array}{rcl}\Gamma_{222}&=&\sum_{d\geq 2} N_d e^{dy_1}\frac{y_2^{3d-4}}{(3d-4)!}\\\Gamma_{112}&=&\sum_{d\geq 1} d^2N_de^{dy_1}\frac{y_2^{3d-2}}{(3d-2)!}\\\Gamma_{111}&=&\sum_{d\geq1} d^3 N_d e^{dy_1}\frac{y_2^{3d-1}}{(3d-1)!}\\\Gamma_{122}&=&\sum_{d\geq 1} dN_de^{dy_1}\frac{y_2^{3d-3}}{(3d-3)!}\end{array}.

Now, we multply things together to get the right hand side’s terms, which are \Gamma_{112}^2=\sum_{d\geq 2}\sum_{d_1+d_2=d} d_1^2N_{d_1}d_2^2N_{d_2}e^{dy_1}\frac{y_2^{3d-4}}{(3d_1-2)!(3d_2-2)!} and also \Gamma_{111}\Gamma_{122}=\sum_{d\geq 2}\sum_{d_1+d_2=d}d_1^3N_{d_1} d_2 N_{d_2} e^{dy_1}\frac{y_2^{3d-4}}{(3d_1-1)!(3d_2-3)!}.

Next up, we equate coefficients of e^{dy_1}\frac{y_2^{3d-4}}{(3d-4)!}, with the factorial precisely what we need to turn the factorials above into binomial coefficients, and we finally get, for d\geq 2, the formula

N_d=\sum_{d_1+d_2=d} N_{d_1}N_{d_2}\left(d_1^2d_2^2\binom{3d-4}{3d_1-2}-d_1^3d_2\binom{3d-4}{3d_1-1}\right). To get all the N_d, we only need to know N_1, the number of lines through two points. This is one we all know, and it’s 1.

The next two numbers are familiar, or at least doable by algebraic geometry grad students: N_2=1, the number of conics through 5 points, and N_3=12, the number of nodal cubics through 8 points. The conic one is rather elementary, it’s just the fact that five hyperplanes in \mathbb{P}^5 intersect in a point. The cubic one is a bit trickier, and can be obtained by noting that the rational cubics are the singular ones, and so form a divisor in the space of cubics, and the condition of passing through 8 points is equivalent to intersecting this divisor with a line in the space of all cubics. There are many, many ways to find that the degree of this divisor is 12, and that’s essentially what’s left. I have no idea how to get the result from quartics without this formula, though I know it CAN be done.

About Charles Siegel

Charles Siegel is currently a postdoc at Kavli IPMU in Japan. He works on the geometry of the moduli space of curves.
This entry was posted in Algebraic Geometry, Big Theorems, Cohomology, Computational Methods, Curves, Enumerative Geometry. Bookmark the permalink.

6 Responses to Kontsevich’s Formula

  1. notedscholar says:
    December 24, 2008 at 6:17 pm

    And you finish with a bang!

    Perhaps you should make a New Years commitment to not be so obscurantist, like John Armstrong, and instead promote the public understanding of math!

    NS
    http://sciencedefeated.wordpress.com/

    Reply

  2. Pingback: best of 2008 (2) : big theorems

  3. csar says:
    February 4, 2009 at 4:41 am

    If we are working on intersections ( an integer basically), why that number “e” showed up? It doesn’t make sense…
    csar

    Reply
  4. csar says:
    February 4, 2009 at 4:50 am

    Besides, you did not say anything about why do the coefficients (the GW-invariants), carry with enumerative information, that’s the hole point of this computation, otherwise there’s no reason you can interpret that number (Kont’s formula), as the number of curves of degree $d$…
    csar

    Reply
  5. csar says:
    February 4, 2009 at 5:02 am

    I didn’t say “please” last time,…sorry about that! but do you know the answer? :)
    cya csar

    Reply
  6. Charles Siegel says:
    February 4, 2009 at 7:42 am

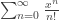    The number “e” only shows up formally, we think of e^{x} as being precisely \sum_{n=0}^\infty \frac{x^n}{n!}, and we had constructed things in such a way to get these terms. The point there is that this is a much easier thing to differentiate and work with than a power series is.

    As for why the GW invariants carry enumerative information, the definition has them as first intersecting a bunch of classes on the moduli space of maps, and then integrating, which essentially counts points. In fact, the lemma at the end of this post says that, generically, the GW invariants are numbers of curves, well, the number of stable maps, which then amounts to the same thing.

    Reply

Leave a comment