The Hilbert Polynomial

Posted on January 9, 2008 by Charles Siegel

Now that we have algebra on our side, we can start doing some real geometry. Today we’ll look at Hilbert Functions, Hilbert Polynomials, and all the very nice invariants we can define with them. These invariants are key to the study of varieties (and, in fact, schemes, which we’ve yet to mention) and are easily calculated with the Hilbert Polynomial, though we will not touch on computation now.


Now let k be an algebraically closed field, and let S=k[x_0,\ldots,x_n] and let M be a graded S-module. We define the Hilbert Function of M to be \varphi_M(n)=\dim M_n. That is, the dimension, as a k-vector space, of the degree n part of M.

Theorem: Let M be a finitely generated S-module. Then there exists a unique polynomial P_M(n) with rational coefficients such that, for all n sufficiently large, P_M(n)=\varphi_M(n). Furthermore, if \mathrm{Ann}(M) is the ideal \{f\in S|f\cdot M=0\}, then \deg P_M(n)=\dim V(\mathrm{Ann}(M)).

Proof: To begin, we define a short exact sequence to be 0\to M'\stackrel{f}{\to} M\stackrel{g}{\to} M''\to 0, a pair of module homomorphisms such that the f is injective, g is surjective, and the image of f consists precisely of the elements of M which are sent to 0 by g. Later, when we talk about exact sequences in general, it will be more obvious why the zeros are there, but for now we’ll just take it as a convention.

We first note the fact that Hilbert Functions and the varieties mentioned in the theorem are both additive in short exact sequences. That is, knowing them for the first and last module gives complete knowledge for the second one. Specifically, if the theorem holds for M',M'', then it holds for M. Taking into account the existence of filtrations discussed last time, we in fact only have to look at modules of the form S/\mathfrak{p} for some prime ideal \mathfrak{p}.

Now, if \mathfrak{p}=(x_0,\ldots,x_n), then it is true, provided that we define the degree of the zero polynomial to be -1 as well as the dimension of the empty set, as the Hilbert Function is zero for positive input. Now we assume that \mathfrak{p} is not (x_0,\ldots,x_n), and that the theorem holds for ideals with varieties of lower dimension. Then there is a short exact sequence 0\to M\to M\to M/x_iM for x_i\notin\mathfrak{p} given by having the first map be multiplication by x_i and the second being the natural quotient map. The last module we will denote by M''.

Using the additivity in short exact sequences, this tells us that \varphi_{M''}(n)=\varphi_M(n)-\varphi_M(n-1) and that V(\mathrm{Ann}(M''))=V(\mathfrak{p})\cap H, where H=V(x_i). This tells us that the dimension of V(\mathrm{Ann}(M''))=\dim V(\mathfrak{p})-1. So the result holds for M''.

Finally, a function such that f(n)-f(n-1) is a polynomial must be a polynomial itself, and so \varphi_M(n) is a polynomial of the appropriate degree. QED

This introduces us to the importance of short exact sequences, things being additive in short exact sequences, and the power of induction. So now, we can define the Hilbert Polynomial to be the polynomial of the theorem.

So now let V be a projective variety. Then we define P_V(n) to be the Hilbert Polynomial of the projective coordinate ring of V. We call this the Hilbert Polynomial of the variety. It encodes a LOT of information. We’ll now define a bunch of invariants that it gives us.

First, we can use the Hilbert polynomial to DEFINE the dimension. Just say that the dimension of a variety is equal to the degree of its Hilbert Polynomial.

Second, we can define the arithmetic genus by p_a(V)=(-1)^{\dim V} (P_V(0)-1). This invariant is especially useful for curves, for reasons that we’ll encounter in the future.

Third, we define the degree of a variety of dimension r to be r! multiplied by the lead coefficient of the Hilbery Polynomial. The degree is roughly the number of times that the variety will intersect a hyperplane of complementary dimension in projective space. We’ll not make this rigorous right now, because rather we’ll do that next time, and use it to prove Bezout’s Theorem.

About Charles Siegel

Charles Siegel is currently a postdoc at Kavli IPMU in Japan. He works on the geometry of the moduli space of curves.
This entry was posted in AG From the Beginning, Algebraic Geometry. Bookmark the permalink.

8 Responses to The Hilbert Polynomial

  1. John Armstrong says:
    January 9, 2008 at 8:13 pm

    We first note the fact that Hilbert Functions and the varieties mentioned in the theorem are both additive in short exact sequences.

    This is clear enough for the Hilbert function if f and g both have degree {0}, but it would be nice to see it done for more general morphisms. Also, in what sense do we “add” annihilators or varieties?

    One thing I’ve never really grokked about the HP is why it doesn’t matter that it disagrees for low n. The degree corresponds to the dimension, in my view, because the degree encodes a growth rate (like big-O notation) of the ranks, and the ranks grow faster with more dimensions to work with. 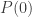But then for the genus you use the polynomial evaluated at {0}, but the theorem doesn’t tell us that P(0) has anything to do with \phi(0)! It always feels a bit like black magic to me.

    Reply
  2. Charles says:
    January 9, 2008 at 10:36 pm

    The sense in which we add annihilators is by taking the union of their varieties.

    It’s important to note that the Hilbert Function/Polynomial depends on the embedding of the variety. Using Groebner bases, it is actually fairly simple to compute the Hilbert Function completely, and you get a linear combination of binomial coefficients plus terms that look like \dim k[x]/x^n for some n, which drop out eventually. As for the genus depending on 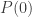P(0), this is precisely because the embedding often screws things up a bit in low degree with those nilpotent variables.

    There’s another way to define the Hilbert Polynomial, which provably gives the same one for projective varieties, by taking the Euler Characteristic of the nth twisted structure sheaf as the value at n. This is exactly the Hilbert Polynomial, without the sporadic beginning (though it’s quite a bit tougher to prove and work out than the classical definition) and it is really where the fact that the genus is dependent on 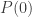P(0) comes from (at least, to me). So the reason we don’t use the Hilbert Function is partly because it’s not as nice as a polynomial…and partly because the sporadic part is too sensitive and makes it harder to extract information. The polynomial, on the other hand, can be directly defined from an intrinsic part of the variety, and so has a closer connection to some intrinsic invariants.

    For the first part, assuming that they have degree zero is enough always, the way to get around it is to shift the grading on the modules, so this works for arbitrary morphisms (that respect grading, at least).

    Reply
  3. Michi says:
    July 9, 2008 at 9:21 pm

    Thanks for this post. Since i’m trying to get a quick grip of some of this stuff it came in very handy. Not having to much background in algebraic geometry though i hope you can answer the following: does the Hilbert polynomial of a homogeneous ideal I in S differ from the Hilbert polynomial of its radical? And could you give me a neat reference for this and the previous post?

    Reply
  4. Charles says:
    July 10, 2008 at 12:33 am

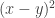    Here’s a kind of stupid example. Look at k[x,y] and the ideal (x-y)^2. This gives the equation x^2=2xy-y^2, so in each degree, we have the quotient generated by xy^{d-1},y^d, so the Hilbert polynomial will be 2.

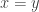    However, look at k[x,y]/(x-y). This is generated in each degree by y^d, with the equation being x=y, and so has hilbert polynomial 1.

    More generally, flat families (which I’ll be heading towards in the not-so-distant future) preserve Hilbert polynomials, and so you can think of it as whether a point can deform to a double point, which it can’t. Two points can, however.

    As for references, I wrote these posts mostly out of section 1.7 of Hartshorne with a bit of Commutative Algebra from Eisenbud.

    Reply
  5. Michi says:
    July 10, 2008 at 9:00 am

    Thanks for your response! Actually I figured it out myself with the same simple example in the equivalent form (x^2) in k[x,y]. Still i hope you don’t mind if i throw another unthought question at you: is there a stronger relation between the Hilbert polynomial of a graded module M over S and the Hilbert polynomial of S/Ann(M), except that they have the same degree?
    It’s a bit vague question but it somehow suggest itself from this filtration of the module you mention in the previous post and the good behaviour of Ann and the Hilbert polynomial under exact sequences. I’ll give it a thought but maybe you already know an answer.

    Reply
  6. Charles says:
    July 10, 2008 at 8:11 pm

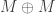    I’m not seeing anything obvious, at least. For instance, the lead term and the value at zero can’t be that closely related, because I can multiply them by any positive integer I like for P_M without changing P_{S/Ann(M)} by noting that the annihilator of M\oplus M and the annihilator of M are the same.

    That’s not saying that there isn’t anything, but nothing is leaping out at me.

    Reply
    • Muhammad Saeed Ahmad , Lecturee in Mathematics. says:
      June 13, 2015 at 10:54 am

      Is the there any meaningful difference between a Hilbert function and a Hilbert Polynomial? I am very much new in commutative Algebra and don’t have any algebraic geometric background….suggest me Books on commutative algebra and algebraic geometry which are easy to read for a new beginner and which include solved concrete examples to understand the concepts properly. If you have your own notes on these subjects email me on my id: saeedkhan099@hotmail.com
      Thanks …………..

      Reply

  7. Pingback: The Hilbert Scheme « Rigorous Trivialities

Leave a comment