I got four people that seemed more-or-less to want me to keep going with these, so I have decided to do it, and not just because it means I have less work to do regarding finding a topic for each post. Anyway, on my post which was an overview of resolution of singularities (which I intend to, at some point, go into more detail on the proof…just need to understand it properly first), John asked about the details of normalization. Right there, I did an example, and here I’m going to do a bit of theory for the process, and then repeat that example and add a second one.
As is often the case in algebraic geometry, we start with the algebra. We say that an integral domain is normal if the roots in the field of fractions of
for every monic polynomial (polynomial with lead coefficient 1) in
are already in
. We’ll start with two examples, and generalize to a theorem. First up, the integers are normal. The field of fractions there is the field
. Now, if you take a monic polynomial with integer coefficients, the only rational solutions you can get are integers again. Similarly, the ring
is normal for any field
. The key thing these two rings have in common is unique factorization (that is, every element can be written uniquely as a product of finitely many elements which cannot be factored further, up to an invertible element). So we can actually prove the following:
Proposition: Any unique factorization domain is normal.
Proof: Any element of , the field of fractions, can be written as
uniquely in lowest terms, because we have a UFD. Now we plug it into a general monic, and we obtain
. Clearing denominators, we get
. A short algebraic manipulation later and we get to
. So then we have
divides
. That would mean that
and
have a common factor, which is a contradiction. QED.
So now we have a class of normal rings. That’s a good place to start from, and seeing that is normal hints that there might be some nice property of affine space that this generalizes to other varieties and schemes. This is, in fact, the case.
We say that a scheme is normal if every local ring is. But to be completely honest, I don’t care much for normal schemes, so we’re going to focus on varieties (in the abstract), which are what really matters. (yes, I’m letting my geometric bias show here, just as I will later if I start working over explicitly again).
An easier definition to check is that a variety is normal if it is covered by open affine varieties which are normal, and an affine variety is normal if and only if its coordinate ring is. So that tells us that is always normal, because it can be covered by
‘s, which have coordinate ring
.
Now, we want to define a normalization of a variety. First we’ll define it with abstract nonsense and a universal property. Let be any variety. A normalization of
is a morphism
such that
is normal and for any other normal variety
and map
a dominant morphism (that is, the image is dense) we get a unique morphism
with
.
Now, it’s not AT ALL obvious that this exists in general. For affine varieties, however, it’s not so hard. Take to be an affine variety, and
its coordinate ring. Then the normalization of
is the affine variety
with
the normalization (in the sense of rings) of
. All this is is that we take all the monics with coefficients in
and then take the ring of solutions to them in
, the field of fractions. That this is a ring is a fairly standard commutative algebra problem, and is left as an exercise (hint: reformulate in terms of modules and note that an element is integral over
if and only if
is a finitely generated
-module). The morphism for normalization of affine varieties is the one given by the inclusion
.
Uniqueness of normalization is pretty easy from the universal property, and in fact, it’s unique up to unique isomorphism. Existence is the tricky part, which we prove below:
Proof of Existence: Let be any variety and
be an open affine cover. For each
, we have a normalization
by taking the normalization of the coordinate ring, and these are affine. Now, as normalizations are unique, we have that
and
must be isomorphic by a unique isomorphism making all the relevant diagrams commute. Thus, we can glue the
together by identifying them along these isomorphisms. This gives us a variety which we will call
. (It does require a check that
is separated, but I’m not going to do it here.) In fact, we get a map
because the gluings were uniquely determined by the conditions of being locally normal, and so they agree on overlaps. Finally, we note that
is in fact normal, and as any dominant map
where
is normal will locally factor through
in a nice way, the whole map factors through, and so we have that
is the normalization. QED
So now normalizations exist for any variety, which means that we can attempt to do things like work on normal varieties and pushforward whatever properties we get to see if we can get something on arbitrary varieties. But we’re left wondering what nice properties do normal varieties have? Well, here’s the big one:
Theorem: The set of singular points of a normal variety has codimension .
Proof: Suppose that is normal of dimension
and let
be the set of singular points. Suppose that it contains a component
of dimension
. Then (and this is nontrivial, but not something I intend to prove, though it is where we actually use the fact that we have a normal variety) there exists an affine open set
such that
is cut out by a single equation. There exists
which is a nonsingular point of
but not of
. Look at
, the local ring of
at
, and
local parameters (that is, their images in
form a basis).
Now, is a principal ideal in
, so
for some
. Similarly, we must have
and
is the inverse image of
under the natural quotient map of local rings. Choose
to be inverse images of
. Then
, and so
, because it is generated by at most
elements. So then,
is a nonsingular point of
, contradicting our assumption that it was. So
has no codimension 1 components. QED.
The value here is that this shows that normal varieties are regular in codimension one, and so we can define Weil divisors for them, and as a geometer, I consider Weil divisor to be better whenever we can use them. Now, if the local rings are all UFDs (which is stronger than normal), Weil divisors and Cartier divisors are the same. However, for normal varieties, Cartier divisors form a subground of Weil divisors. The other nice thing this does is prove that curves admit resolutions, that is, every curve is birational to a nonsingular curve. This is simply the normalization of a curve, as the singularities are in codimension 2, and that’s the empty set, there can be no singularities on a normal curve.
So now, as promised, some examples of normalization. Both will be simple normalizations, in fact, both are rational curves, and I’m choosing the simplest singularities out there, the cuspidal cubic and the nodal cubic.
Example 1: The cuspidal cubic curve is defined by the equation in the plane. It thus has coordinate ring
, which is isomorphic to
by
and
. Now, once we find a normal ring that contains
and is contained in the normalization, we’re done. Such a ring is
, because
is a monic polynomial with coefficients in
and it has
as a root in the field of fractions, which is
. So then,
must be the normalization, and so the normalization of the cuspidal cubic curve
is
given by taking the point
to
in the plane.
Example 2: The nodal cubic is defined by
. Here we don’t have as nice a characterization of the coordinate ring, so we need to work a bit less directly. Look at the parameter
on the curve. So then in the field of fractions, the equation can be reduced to
by dividing by
. The point of that is that now we have that
, which is monic with coefficients in
is zero, and so
is in the normalization. Now, if we take any element integral over
, it can be written as a polynomial in
, as any instance of
becomes
and any instance of
becomes
. Thus,
is the integral closure, so again
is the normalization map. Note that along the way we showed that
, and from there it is a bit clearer that
is the normalization.

Speaking as the long term lurker of a wide variety of math and science blogs (mostly math), I can say there’s at least 5, and likely quite a few more, who would be interested in more in the series ;).
Keep up the good work!
I second what Robert said, though I won’t have much time to read any of the new entries for a few weeks.
Hi,
I am a beginner in algebraic geometry. May I know why we care about normalization in general? Is it because of resolution of singularity? Forgive my stupidity, but what motivates one to consider integrally closed domains when one tries to remove a singularity? I have no intuition about this at all.
Thanks!
Soarer, part of it is resolution of singularities, but also part of it is that for other things normal varieties are easier to work with, and although they are a special case, every variety can be normalized, so it’s a special case we can often reduce to in order to finish proofs.
Thanks for your reply.
Can you be more precise when you say that normal varieties are easier to work with? Any examples?
Well, Weil divisors require that things be regular in codimension one in order to define them, and normal varieties always are. So you don’t need to worry about added difficulties for Cartier Divisors.
So maybe I should look at it as something that easily implies regular in codimension 1. Thanks.
That’s how I tend to view it. There are some other situations in which normality helps, but that’s the big one, to me: all singularities have codimension at least 2.
Hi, this is the second I find some hope on the net and more precisely in your page. Thank you for that. I am trying to prove a universal property (although in the analytic case) for the normalization of a space and I am trying to do it using only the corresponding rings. Given a normal variety W and a map from W to a variety V, there exists a uniquely determined map from W to the normalization of V. Any ideas?
Ups, I am sorry. I was trying to say: this is the second TIME I find some…
Thank you again.
Well, pass to the affine case, then you have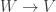 with
with  normal. This is the same as a map
normal. This is the same as a map ![k[V]\to k[W]](https://s0.wp.com/latex.php?latex=k%5BV%5D%5Cto+k%5BW%5D&bg=ffffff&fg=333333&s=0&c=20201002) with
with ![k[W]](https://s0.wp.com/latex.php?latex=k%5BW%5D&bg=ffffff&fg=333333&s=0&c=20201002) integrally closed. You’re going to need, I think, a dominant map, so that this map of affine rings is an inclusion, and then you’ve got a ring inside of an integrally closed ring, and so the integral closure fits in the middle, and that’s it.
integrally closed. You’re going to need, I think, a dominant map, so that this map of affine rings is an inclusion, and then you’ve got a ring inside of an integrally closed ring, and so the integral closure fits in the middle, and that’s it.
OK, I’ll try to pass your idea to the analytic case. Thanks!
Hey! I love your blog. Please keep going. Im taking a rather advanced alg geometry class and this is really helping me…
How much do we know about normal singularities?
For example, Are all toric singularities (Which of course happen at co-dimension two or higher) normal?
(reference please)
I’m not an expert on singularity theory, but I recommend that you formulate a more specific question than the first one (the second might be ok) and ask it at mathoverflow.net.
This only depends on whether or not you assume toric varieties are normal doesn’t it?
Pingback: Aprenda un poco de inglés con… Rigorous Trivialities | Blog del Departamento de Álgebra
Pingback: Rosenlicht unit theorem-II « Problem by problem
May I ask what is the sheaf of conductors for this example of a nodal curve?
Hi, do you have a reference for the normalization of a real analytic variety? Everything I could find in the litterature is made over an algebraically closed field, or only for affine real algebraic varieties.