Last time, we talked about , which takes rings and gives us affine schemes in a manner analogous to affine varieties. Now, though it is safe to say that projective varieties are schemes (well, with the extra points taken into account) because they are covered by affine varieties (and so affine schemes), they’re actually MUCH nicer than arbitrary schemes. So, we’re going to discuss
which takes graded rings to special types of schemes.
The analogies between projective varieties and for a graded ring
are the same as those between affine varieties and
. To start with, we take
a graded ring. There is a distinguished ideal in
called the irrelevant ideal, it is given by
. So we take the set
to be the set of homogeneous prime ideals not containing the irrelevant ideal. Now, why do we throw out this irrelevant ideal? Let’s look at the case of
. We want Proj of this to be projective space. The irrelevant ideal is then
, which requires that all the homogeneous coordinates vanish. However, this isn’t a point in projective space, so we want to ignore it in general. Additionally, the primes that are maximal among those not containing the irrelevant ideal will correspond to the points of a projective variety. In
, we take the point
, then the ideal of the point is given by the linear equations of the form
, and is maximal among this set.
So we have our point set. We’ll get our closed sets in the same way as before: let be a homogeneous ideal, then
is a closed set. This gives us a topology on
. All that remains is to define the structure sheaf. We define the distinguished open sets of
as follows: given
a homogeneous element of
of degree one, we define the distinguished open given by
to be
. The distinguished opens cover the space, and so we can define a sheaf by giving it on these open sets. To the distinguished open
determined by
, we assign the ring
, that is, the degree 0 elements of
. Similarly to the affine case, this procedure will give for projective varieties the original structure sheaf.
So now we’ve defined Proj. We step back and work with both affine and projective schemes for a moment. Let be a ring. Then we make the convention that
is called
and that
is called
. These two schemes are related just as we would expect from varieties:
can be thought of as
.
We’ve spoken about subvarieties, so now what about subschemes? We’ll need a subset which has, in the subspace topology, a sheaf, and we’ll even want it to relate to the original one in some nice manner. Let and
be schemes. We define a morphism
of schemes to be a morphism of locally ringed spaces. Now, an open subscheme of
will just be an open subset
whose structure sheaf is the restriction of that of
. So then an open immersion will just be a morphism
such that it induces an isomorphism of
with an open subscheme of
.
More interesting is the case of closed subschemes. Here, we must first define a closed immersion, which is a map such that it induces a homeomorphism of
onto a closed subset of
and such that the induced map on sheaves is surjective. Then a closed subscheme is an equivalence class of closed immersions, where
and
are equivalent if we have
an isomorphism such that
. Now this sounds complicated, but really this just says that we’re identifying the subset up to automorphism. After all, what’s the difference between parameterizing the x-axis from left to right and from right to left? We’ll just treat them as the same. As for closed immersion, it’s saying that a closed immersion is given by a sheaf of ideals, so this really is a good definition of closed subscheme to have generalizing the notion of a subvariety.
This, in fact, tells us that the closed subschemes of are of the form
for an ideal
, and that the same holds for
with the caveat that
must be homogeneous.
Now, we’ll talk about the properties that let us distinguish our abstract varieties from arbitrary schemes. I’ll start out by just saying what a variety is, and then we’ll go for each word individually. A variety is an integral separated scheme of finite type over an algebraically closed field . The first word is easy: an integral scheme is any scheme whose structure sheaf consists only of integral domains. This has the nice property that a scheme is integral if and only if it is irreducible as a topological space and all the rings have no nilpotents.
Now we’re going to skip to the “over ” part. Let
be a scheme. Then we say that
is a scheme over
, that is, a scheme with a map to
. The ability to do things like this is extremely important, and we call
the base that we are working over. Many powerful theorems are proved using a method called base change. The idea there is that we have
and
and we’d like to work over
instead. So we take the fiber product
and call it
, and we have a map
. Then the problem is reduced to checking the property for
and checking that it is preserved by base change. Now, to make sense of the notation, whenever
happens to be of the form
, we often say that
is a scheme over
as a convention. So this just means that a variety comes with a map to
, that is, a point with structure sheaf
. The map to the point is easy, and the last part says that the structure sheaf consists of
-algebras, and that’s what we’d prefer to have.
Next up is separated. This will be quick, because we’ve discussed it before as the difference between prevarieties and varieties (this is why people used to call arbitrary schemes preschemes: they kept the word scheme for the separated ones). Now we can actually say what it means for a morphism to be separated. A morphism is separated if the diagonal morphism
, which is the unique morphism whose composition with both projections is the identity map on
, is a closed immersion. So what we really mean above is that
is separated over
, that is, the morphism
is separated, which means that
is a closed immersion. The truth of the matter is, we’ve been secretly taking fiber products over
the whole time, because we have a unique map there for varieties, so this is precisely the condition we started with.
Now the tricky one: of finite type. This is again a property of the morphism . We define a morphism of schemes
to be locally of finite type if there is a covering of
by open affine subsets
whose preimages are covered by open affines
where
is a finitely presented
-algebra. The morphism if of finite type if we can do this with finitely many
‘s for each
. So this says that the preimage of this structure map, which is the whole variety, can be covered by finitely many affine vareities.
Taken all together, these conditions say the following: of finite type over tells us that our space is covered by finitely many affine varieties, then the integral condition requires that there be no nilpotent functions and that it be irreducible, and finally separatedness moves our prevariety into the realm of being an actual variety, so we have our old class singled out in this way from the more general collection of schemes. We even can get back down to projective varieties by requiring that we look at the Proj of a graded ring on top of things, so inside of the big category of schemes we can find the varieties that we know and love.

For a closed immersion, the map on sheaves should be surjective. Also, the decomposition of P^n into A^n \union P^(n-1) (which involves a choice) identifies A^n with {P^n – V(x_0)} and the “coordinates” become x_i = x_i/x_0 for i > 0 (in your notation). Also I apologize for not knowing how to type math remarks into the comments….
Ack, I was thinking surjective and wrote injective by accident, it’s fixed now. And yeah, the decomposition of isn’t in any way, shape or form natural, but it’s something that we do over
isn’t in any way, shape or form natural, but it’s something that we do over  to help think geometrically about it, so it’s good to know that we can do it over any ring at all.
to help think geometrically about it, so it’s good to know that we can do it over any ring at all.
Pingback: Flattening Stratifications « Rigorous Trivialities
I would like to ask about closed subschemes. I know that in affine case, a closed subscheme of SpecA is pretty much Spec A/I for some ideal I. Now as it is possible to have rad I = rad J, so we would have possibly different sheaves on the same topological space.
My question is about how we should view these different sheaves. I don’t really understand the role of nilpotents here. (I’ve looked up Eisenbud and Harris but I don’t quite understand the embedded point part..) Is it possible for you to explain a little bit on this? Thanks!
Well, one thing that this stuff can encode is multiplicity and tangent information. Here’s an example.
Let![A=k[x,y]](https://s0.wp.com/latex.php?latex=A%3Dk%5Bx%2Cy%5D&bg=ffffff&fg=333333&s=0&c=20201002) ,
,  and
and  with
with  . The ring for their intersection is
. The ring for their intersection is ![k[x,y]/(x-t,y^2-x)](https://s0.wp.com/latex.php?latex=k%5Bx%2Cy%5D%2F%28x-t%2Cy%5E2-x%29&bg=ffffff&fg=333333&s=0&c=20201002) . For
. For 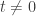 , this is a reduced scheme, and is in fact a variety consisting of two points,
, this is a reduced scheme, and is in fact a variety consisting of two points,  .
.
However, look at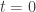 . Then we have
. Then we have ![k[x,y]/(x,y^2-x)=k[x,y]/(x,y^2)\cong k[y]/y^2](https://s0.wp.com/latex.php?latex=k%5Bx%2Cy%5D%2F%28x%2Cy%5E2-x%29%3Dk%5Bx%2Cy%5D%2F%28x%2Cy%5E2%29%5Ccong+k%5By%5D%2Fy%5E2&bg=ffffff&fg=333333&s=0&c=20201002) . So it’s a single point, but instead of having a field of regular functions, it has a ring which is a two dimensional vector space over the field, and so the point should count as intersection with multiplicity 2. This direction leads to intersection theory, and is well illustrated by writing out a scheme theoretic proof of Bezout’s Theorem.
. So it’s a single point, but instead of having a field of regular functions, it has a ring which is a two dimensional vector space over the field, and so the point should count as intersection with multiplicity 2. This direction leads to intersection theory, and is well illustrated by writing out a scheme theoretic proof of Bezout’s Theorem.
However, we might also want to look at![k[x,y]/(x,y^2)](https://s0.wp.com/latex.php?latex=k%5Bx%2Cy%5D%2F%28x%2Cy%5E2%29&bg=ffffff&fg=333333&s=0&c=20201002) , as a subscheme of
, as a subscheme of ![k[x,y]](https://s0.wp.com/latex.php?latex=k%5Bx%2Cy%5D&bg=ffffff&fg=333333&s=0&c=20201002) . In which case we note that it is contained in the scheme defined by
. In which case we note that it is contained in the scheme defined by 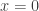 , which is the
, which is the  -axis, or
-axis, or ![k[y]](https://s0.wp.com/latex.php?latex=k%5By%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Even better, we need to note that (and I’m not proving it in a comment) tangent vectors to a point
. Even better, we need to note that (and I’m not proving it in a comment) tangent vectors to a point 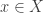 are maps
are maps ![\mathrm{Spec}(k[\epsilon]/\epsilon^2)\to X](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpec%7D%28k%5B%5Cepsilon%5D%2F%5Cepsilon%5E2%29%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) which map the closed point to
which map the closed point to  . In our case, that’s the same as a map
. In our case, that’s the same as a map ![k[x,y]/x\to k[\epsilon]/\epsilon^2](https://s0.wp.com/latex.php?latex=k%5Bx%2Cy%5D%2Fx%5Cto+k%5B%5Cepsilon%5D%2F%5Cepsilon%5E2&bg=ffffff&fg=333333&s=0&c=20201002) , which is accomplished by
, which is accomplished by  . So we not only get a point, but we get a tangent vector, which tells us that the line
. So we not only get a point, but we get a tangent vector, which tells us that the line 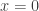 is tangent to
is tangent to 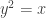 , and in the
, and in the  -direction, which is clear geometrically.
-direction, which is clear geometrically.
Did that help?
That helps, thanks!