Sorry about the extended delay, should be back to regular Monday-Wednesday-Friday updates now. I hope. Anyway, we’re going to be heading into Intersection Theory soon, and in particular we’re going to be looking at surfaces. Sadly, at this point, abstract varieties aren’t good enough anymore. We’re going to need all sorts of “non-reduced” behavior, that is, nilpotent functions on our more generalized notion of varieties. This will, however, give us a rather nice way of interpreting Cartier Divisors, or at least the effective ones, so now we’ll just have to get started.
We will start with a motivational example. Let be an affine variety. Then look at
, the affine coordinate ring. We can recover the variety from the ring, completely, so let’s see how to do it. First, we define a set with no extra structure and call it
. This is the set of maximal ideals of
. These correspond to the points of the variety, because maximal ideals are minimal subvarieties, and so are points.
Next up we need a topology. Let . Then we can look at the number given by
in
for each maximal ideal
. These just correspond to the values of the function. So we can take the sets where
gives a nonzero number to be open, and take the collection of these sets to form a basis for the topology and these are just the sets where functions don’t vanish. We get the same topology we started with. We will call these open sets the distinguished opens.
And the last piece in giving a variety has to be the sheaf of regular functions. It is a theorem (well, really a lemma) that if you give the values of a sheaf on a base for the topology, then that uniquely determines the sheaf. So we only need to worry about the distinguished opens. We have a natural algebraic choice here: the open set is determined by being nonzero, so we can take
to be an invertible element. That is, we assign the localization
. These are just the rational functions on
which are defined away from the locus where
, so this is the sheaf we wanted. We have our variety back!
Now, we can generalize slightly before generalizing massively. Instead of using which takes the maximal ideals, let’s look at
, the set of all the prime ideals. This contains the original, but has a few extra points. We’re going to make a switch from worrying about open sets to the closed sets. The closed sets of
are given by
, where
is an ideal. Why this definition? Back to varieties: given an ideal
, its zero set is going to be the points whose maximal ideals contain
, because then the ideal is sent to zero in the quotient. This just replaces the word “maximal” with “prime.” And of course, the open sets are the complements of the closed sets, and the distinguished opens are the complements of the zero sets of principle ideals.
So we have a set with a topology, what about the sheaf? If we denote the distinguished open defined by to be
, then we assign to
to ring
, just as before. We don’t change anything at all here.
So what’s the point of all this? Well, in the last version above, where we looked at all prime ideals, we never made use of the fact that our ring was a finitely generated -algebra with no zero divisors. Not once. What did we use? We used that
is a commutative ring with identity. That’s it, nothing more. This definition works for any ring, so we might as well make use of it. Such a thing is called an affine scheme.
So now it’s really easy to define a general scheme: a scheme is a locally ringed space which is locally isomorphic to affine schemes. (In the older literature, it’s sometimes called an prescheme, but we will follow modern convention.)
Now, schemes are the heavy duty powerhouses of algebraic geometry. We’ll not go into the more generalized spaces like algebraic spaces or algebraic stacks (at least, I don’t think I’ll be going in that direction), so schemes are the greatest generality we’ll work with. Now, back when I introduced abstract varieties, John asked about things we can do in that category that we can’t in the original category of projective varieties. Well, here we actually get a major expansion: fibered products (also called pullbacks) exist. I’m not going to prove this, because it’s rather involved and I really don’t want to, but the general idea is to locally patch together tensor products.

:P
I’d like to see someone work out, in detail, a simple example of varieties whose pullback doesn’t exist as a variety, but where it does exist as a scheme. Show me exactly where schemes let you work around the bad parts.
I plan to do just that when we cover families of varieties at some point in the future. The standard example is the family over given by
given by ![\mathrm{Spec}(k[x,y,t]/(x^2-ty))](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpec%7D%28k%5Bx%2Cy%2Ct%5D%2F%28x%5E2-ty%29%29&bg=ffffff&fg=333333&s=0&c=20201002) of parabolas. The fibers of a morphism can be viewed as fiber products (we’ll discuss how in the future) and that makes the fiber of this map over
of parabolas. The fibers of a morphism can be viewed as fiber products (we’ll discuss how in the future) and that makes the fiber of this map over 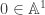 the scheme
the scheme ![\mathrm{Spec}(k[x,y]/x^2)](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpec%7D%28k%5Bx%2Cy%5D%2Fx%5E2%29&bg=ffffff&fg=333333&s=0&c=20201002) , which has a nilpotent function, and so cannot be a variety, but is an affine scheme.
, which has a nilpotent function, and so cannot be a variety, but is an affine scheme.
Pingback: Proj of a Graded Ring and Basic Properties of Schemes « Rigorous Trivialities
Pingback: Cohomology of Sheaves « Rigorous Trivialities
Pingback: Schemes in algebraic geometry I : the affine plane « Embûches tissues
Pingback: Resolution of Singularities « Rigorous Trivialities
Pingback: Varieties and Schemes Revisited | Theories and Theorems