Today, we’re going to prove a BIG theorem, but only in the characteristic zero case (we’ll be working over as usual). The theorem is rather tough, and to do it in positive characteristics it’s best done through stacks. Specifically, we’ll be proving the irreducibility of the moduli space of curves of genus
.
For a start, let be a curve of genus
,
. Then Riemann-Roch tells us that
. This can be rearranged to give
. We want this to be greater than or equal to two, so that we can projectivize and get a map to
. So then we get
. If
, then the inequality is satisfied, so that means that EVERY curve of genus
has a map
of degree
.
So, how ramified is such a cover? Every covering of must be ramified, because otherwise we’d have a covering of a simply-connected space, and it would just be
again. So we apply Riemann-Hurwitz. This tells us that
, and so
, so the map has ramification degree
.
Now, here’s the structure of our argument: there exists a moduli space parameterizing the pairs
where
is a genus
curve and
is a degree
map. What we showed above is that for
, we have a surjective map to the moduli space of curves of genus
,
. So, to prove the irreducibility of
, it would suffice to prove it for
.
But then, there’s a dense open subset of , we’ll call it
, consisting only of the maps with simple ramification. That is, they’ve got
branch points in
. Then, we can take
copies of
and remove the diagonal and call if
. So we’ve got a map
by sending a cover to it’s branch locus. This map is surjective, because (modulo details, of course) if we remove
arbitary points from
, we can then take a
uple cover, because the fundamental group is large, and then connect the sheets to have the correct ramification data over the removed points by a hole-patching procedure to compactify the covering open Riemann surface. Let’s leave actually doing that as an exercise.
All that remains now is to prove that this is actually a connected covering space. Pick a base point in and look at the preimages. It suffices to show that the monodromy representation acts transitively on this fiber, as that means that there is a loop on
that lifts to a path between any two given points in the fiber, which forces path-connectedness. To do this, we’ll work out the action of what happens when two branch points exchange locations.
Let be a point that isn’t a branch point. Define the branch cuts used to glue together a Riemann surface by taking arcs from the branch points to
. Now, to exchange two of the branch points, we’ll have to pass one of the cuts through the other! This seems like a horrible, nasty thing at first, but then, you can realize that they’re just going to give you new transpositions. Why were they transpositions? Because the cuts give a way to get from one branch to another, but only two come together there, so a transposition labels each branch point with that data. Now, if you pass one branch through another, it picks up conjugation by the stationary one, because the cut passes to a different sheet, and will then interchange different sheets of the cover. For instance, if
passes through
, it won’t be acting on sheets in the order 1,2,3 anymore, but in the order 3,2,1, and so will become
. This gives us an action on the fibers, and just fiddling with permutations a bit, it’s transitive. Thus, we have a connected covering space.
Now, a connected covering space of an irreducible space (which certainly is) must be irreducible, and so we’re done!
This post is an imperfect phrasing of pictures I have in my head. If you have any significant suggestions for improvements, please leave a comment.

I think that you mean d = g + 1, not 4g?
You’re right. The degree is , it’s that I’m looking at configurations of
, it’s that I’m looking at configurations of 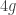 points in
points in  . Fixed.
. Fixed.
Why is a connected covering space of an irreducible space irreducible?